DIP

-

 


Exp-1: Study of MATLAB software and its basic commands.

 

MATLAB (Matrix Laboratory) is a high-level programming language and environment used primarily for numerical computing, data analysis, algorithm development, and visualization. It is widely used in academia and industry for tasks involving mathematics, engineering, and scientific computations.

 

Key Features of MATLAB:

 

1.     Interactive Environment: MATLAB provides an interactive platform to execute commands and visualize data.

2.     Matrix Operations: Built-in support for matrix and array mathematics.

3.     Rich Visualization: Easy-to-use functions for plotting and visualizing data.

4.     Extensive Toolboxes: Additional toolboxes are available for various applications (e.g., Signal Processing, Image Processing, Machine Learning).

5.     Cross-Platform: MATLAB runs on Windows, macOS, and Linux.

 

Basic Commands in MATLAB

 

1.  Variable Assignment

 

x = 10;       % Assigns the value 10 to variable x y = 5; % Assigns the value 5 to variable y

 

2.  Arithmetic Operations

 

sum = x + y;       % Addition difference = x - y; % Subtraction product = x * y;             % Multiplication quotient = x / y;    % Division

power = x^2;        % Exponentiation (x squared)

 

3.  Creating Matrices and Vectors

 

A = [1, 2; 3, 4];          % 2x2 matrix

B = [5, 6; 7, 8];          % Another 2x2 matrix

C = [1, 2, 3, 4, 5];       % Row vector

D = [1; 2; 3; 4; 5];       % Column vector

 

4.  Matrix Operations

 

C_sum = A + B;           % Matrix addition

C_diff = A - B;          % Matrix subtraction C_product = A * B;     % Matrix multiplication C_transpose = A';      % Transpose of matrix A C_inverse = inv(A);    % Inverse of matrix A

 

5.  Accessing Elements

 

element = A(1, 2);       % Access element at row 1, column 2 row_vector = A(1, :);  % Access all elements in row 1 column_vector = A(:, 2); % Access all elements in column 2


6.  Basic Functions

 

mean_value = mean(A(:)); % Calculate mean of all elements in A

std_dev = std(A(:));      % Calculate standard deviation of elements in A max_value = max(A);    % Find the maximum value in A

 

7.  Plotting

 

x = 0:0.1:10;             % Create x values from 0 to 10 with a step of 0.1 y = sin(x);   % Compute y values as the sine of x

figure;                  % Create a new figure window

plot(x, y);              % Create a 2D plot xlabel('x-axis'); % Label for x-axis ylabel('y = sin(x)');    % Label for y-axis title('Sine Wave');            % Title of the plot

grid on;                 % Display grid on the plot

 

8.  Control Flow

 

% If-Else Statement if x > 5

disp('x is greater than 5');


else end


 

disp('x is less than or equal to 5');


% For Loop

for i = 1:5

disp(['Iteration: ', num2str(i)]);

end

 

% While Loop count = 1; while count <= 5

disp(['Count: ', num2str(count)]); count = count + 1; % Increment count

end

 

9.  Functions

 

% Define a simple function function output = square(num)

output = num^2; % Square the input number

end

 

% Call the function

result = square(4); % result will be 16

 

Conclusion

 

MATLAB is a powerful tool for engineers and scientists. Understanding its basic commands is essential for effectively using the software. These basic commands provide a foundation for using MATLAB effectively. Familiarizing ourself with these commands will help you perform a wide range of numerical and graphical tasks in MATLAB.




Exp 2: Write a program to generate and modify matrices using standard commands in MATLAB.


Code:-

% Step 1: Create a 2x2 matrix

A = [1 2; 3 4];

disp('Matrix A:');
disp(A);

 

% Step 2: Change an element (1st row, 1st column)

 A(1, 1) = 10;

disp('Matrix A after modification:');
disp(A);




 


Exp 3: Write a program to perform matrix operations in MATLAB.


Code:-


% Create two 2x2 matrices

A = [1 2; 3 4];

B = [5 6; 7 8];

disp('Matrix A:');
disp(A);
disp('Matrix B:');
disp(B);

 

% Subtract the matrices

C = A - B;

disp('Matrix Subtraction (A - B):');
disp(C);

 

% Matrix Addition

D = A + B;

disp('Matrix Addition (A + B):');
disp(D);

 

% Matrix Multiplication
E = A * B;

disp('Matrix Multiplication (A * B):');
disp(E);

 

 

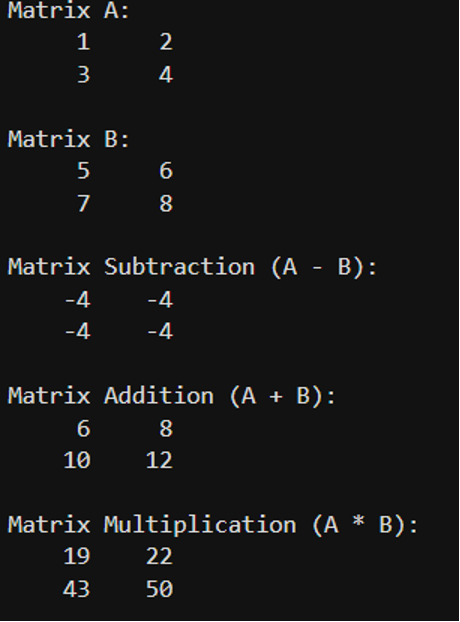
 Output: -




Exp 4: write a program to generate plot using MATLAB.


Code: -


% Create x and y data
x = 0:0.1:10;

y = sin(x);

 

% Generate the plot
plot (x, y);


>> % Create x and y data
x = 0:0.1:10;

y = sin(x);

 

% Generate the plot
plot (x, y);

 

% Add labels
xlabel('x');

ylabel('sin(x)');


Output:-



Exp 5: Write a program to read an image, convert it in grayscale and black & white image, show image in MATLAB.


Code:-


% Step 1: Read the image

img = imread('Screenshot 2024-11-29 at 11.39.21 AM.jpeg');

 

% Step 2: Convert the image to grayscale

gray_img = rgb2gray(img);

 

% Step 3: Convert the image to black and white (binary image)

bw_img = imbinarize(gray_img);

 

% Step 4: Display the original, grayscale, and black & white images

figure;

imshow(img);
title('Original Image');

 

figure;
imshow(gray_img);

title('Grayscale Image');

 

figure;
imshow(bw_img);

title('Black & White Image');


Output:-



Exp 6: Write a program to perform various mathematical operations on image in MATLAB.

 

Code:-

 

% Load the image


image = imread('Screenshot 2024-11-29 at 11.39.21 AM.jpeg'); % Replace with your image file
grayImage = rgb2gray(image);   % Convert to grayscale for simplicity

 

% Display the original image

figure;

subplot(2,3,1);
imshow(grayImage);
title('Original Image');

 

% Brightness Adjustment


brightImage = grayImage + 50; % Increase brightness by adding constant value
subplot(2,3,2);

imshow(brightImage);
title('Brightness Adjusted');

 

% Contrast Enhancement


contrastImage = imadjust(grayImage, [0.3 0.7], [0 1]); % Enhance contrast
subplot(2,3,3);

imshow(contrastImage);
title('Contrast Enhanced');


% Edge Detection


edgeImage = edge(grayImage, 'Sobel'); % Apply Sobel edge detection
subplot(2,3,4);

imshow(edgeImage);
title('Edge Detection');

 

% Image Negation


negativeImage = 255 - grayImage; % Subtract pixel values from 255
subplot(2,3,5);

imshow(negativeImage);
title('Negative Image');

 

% Image Blurring (using Gaussian filter)


h = fspecial('gaussian', [5 5], 2); % Gaussian filter
blurredImage = imfilter(grayImage, h, 'replicate');
subplot(2,3,6);

imshow(blurredImage);
title('Blurred Image');

 

 

 

Output:-




Exp 7: Write a program to find image negative in MATLAB. 

Code:-


% Step 1: Read the original image

img = imread('Screenshot 2024-11-29 at 11.39.21 AM.jpeg');

 

% Step 2: Convert to grayscale if the image is colored

if size(img, 3) == 3

img = rgb2gray(img); % Convert RGB to grayscale

end

 

% Step 3: Find the negative of the image


negative_img = 255 - img; % Subtract pixel values from 255

 

% Step 4: Display the original and negative images

figure;

 

% Original Image

imshow(img); 

title('Original Image');


% Negative Image

figure; 

imshow(negative_img); 

title('Negative Image');


output:-






Exp 8: Apply power law transformation for following image. Analyse result.

 

 

Code:-


% Step 1: Read the original image

img = imread('Screenshot 2024-11-29 at 11.39.21 AM.jpeg');


% Step 2: Convert to grayscale if the image is colored

if size(img, 3) == 3

    img = rgb2gray(img); % Convert RGB to grayscale

end


% Step 3: Normalize the image to the range [0, 1]

img_normalized = double(img) / 255;


% Step 4: Apply Power-Law Transformation

c = 1;    % Constant value

gamma = 2;  % Change this value to adjust brightness (e.g., 0.5, 1, 2)

transformed_img = c * (img_normalized .^ gamma); % Power-law transformation


% Correct: Normalize the result to [0, 1] before scaling

transformed_img = mat2gray(transformed_img); % Normalize


% Step 5: Convert the transformed image back to uint8

transformed_img = uint8(transformed_img * 255); % Scale back to [0, 255]


% Step 6: Display the original and transformed images

figure;


% Original Image

imshow(img);

title('Original Image');


% Transformed Image

figure;

imshow(transformed_img);

title('Power-Law Transformed Image (gamma = 2)');


Output:-





Analyzing the Result:

 

·       Effect of Gamma:

 

·       A gamma value of less than 1 (e.g., 0.5) will brighten the image, especially the darker regions, which can help in enhancing details in shadowed areas.

·       A gamma value greater than 1 (e.g., 2) will darken the image, enhancing the bright areas, which can lead to better contrast in images with significant brightness variation.

 

 

 

Exp- 9 : Write MatLab code to plot histogram of a image and apply histogram equalization on the same image.

Code:-


% Reading the image

image = imread('Screenshot 2024-11-29 at 11.39.21 AM.jpeg');

image = rgb2gray(image); % Convert to grayscale if it's a color image

 

% Plotting original image and its histogram figure;

 

% Displaying the original image subplot(2,2,1);

imshow(image); title('Original Image');

 

% Displaying the histogram of the original image subplot(2,2,2);

imhist(image);

title('Histogram of Original Image');

 

% Applying histogram equalization equalizedImage = histeq(image);

 

% Displaying the histogram-equalized image subplot(2,2,3);

imshow(equalizedImage); title('Histogram Equalized Image');

 

% Displaying the histogram of the equalized image subplot(2,2,4);

imhist(equalizedImage); title('Histogram of Equalized Image');


Output:-




Exp 10: Apply different size averaging filter on an Image and compare results. 

Code:-


% Reading the image

image = imread('Screenshot 2024-11-29 at 11.39.21 AM.jpeg');

image = rgb2gray(image); % Convert to grayscale if it's a color image

 

% Define filter sizes

filterSizes = [3, 5, 7];

 

% Displaying original and first filtered image on first page with larger figure

figure(1);

set(gcf, 'Position', get(0, 'Screensize')); % Set figure to full screen

 

subplot(1,2,1);

imshow(image, 'InitialMagnification', 'fit'); % Display original image
title('Original Image', 'FontSize', 14); % Increase title font size

 

% Applying and displaying the first filter size


h = fspecial('average', filterSizes(1));

filteredImage1 = imfilter(image, h, 'replicate');
subplot(1,2,2);

imshow(filteredImage1, 'InitialMagnification', 'fit');
title([num2str(filterSizes(1)) 'x' num2str(filterSizes(1)) ' Filter'], 'FontSize', 14);

 

% Displaying the next two filtered images on the second page

figure(2);

set(gcf, 'Position', get(0, 'Screensize')); % Set figure to full screen

 

% Applying and displaying the second filter size

subplot(1,2,1);

h = fspecial('average', filterSizes(2));
filteredImage2 = imfilter(image, h, 'replicate'); imshow(filteredImage2, 'InitialMagnification', 'fit');

title([num2str(filterSizes(2)) 'x' num2str(filterSizes(2)) ' Filter'], 'FontSize', 14);

 

% Applying and displaying the third filter size subplot(1,2,2);

h = fspecial('average', filterSizes(3)); filteredImage3 = imfilter(image, h, 'replicate');
imshow(filteredImage3, 'InitialMagnification', 'fit');
title([num2str(filterSizes(3)) 'x' num2str(filterSizes(3)) ' Filter'], 'FontSize', 14);






Exp 11: Apply homomorphic filtering on any appropriate image 

Code:-


% Load and convert the image to grayscale

img = imread('Screenshot 2024-11-29 at 11.39.21 AM.jpeg'); % Replace with your image file


if size(img, 3) == 3

    img = rgb2gray(img); % Convert to grayscale if it's a color image

end


img = im2double(img); % Convert to double for processing


% Perform logarithmic transformation

logImage = log(1 + img);


% Design a high-pass Butterworth filter for frequency domain

[M, N] = size(img);

[u, v] = meshgrid(1:N, 1:M);

u = u - ceil(N/2);

v = v - ceil(M/2);


D = sqrt(u.^2 + v.^2);


D0 = 30; % Cutoff frequency

n = 2;  % Order of the filter


H = 1 ./ (1 + (D0 ./ (D + eps)).^(2 * n)); % High-pass Butterworth filter

H = fftshift(H); % Center the filter


% Perform FFT on the logarithmic image

FFTImage = fft2(logImage);


% Apply the filter

FilteredFFTImage = H .* FFTImage;


% Perform inverse FFT and exponential transformation

FilteredImage = real(ifft2(FilteredFFTImage));

FilteredImage = exp(FilteredImage) - 1;


% Normalize the output image for display

FilteredImage = mat2gray(FilteredImage);


% Display results

figure;

subplot(1, 2, 1);

imshow(img);

title('Original Image');


subplot(1, 2, 2);

imshow(FilteredImage);

title('Homomorphic Filtered Image');

 

 

 

Output:-


















Comments

Post a Comment

Popular posts from this blog

JAVA

-
   S.no Date   Signature 1 15/1/2024 WAP   to   print   your   name   in   Java.   2 15/1/2024 WAP   to   add   2   numbers.   Take   Input   (Via   Command   Prompt   & Via Scanner Class).   3 15/1/2024 WAP to do addition, subtraction, multiplication and division by taking (Values for variables & Values via Scanner Class).   4 29/1/2024 WAP   to   calculate   factorial   of   a   number   taken   via   Scanner  Class.   5 29/1/2024 WAP to take 5 numbers as an input from the user and then calculate   (Average   of   the   number   &   Maximum   and   minimum among the numbers).   6 29/1/2024 WAP   to   take   2   numbers   and   a   symbol   (+,   -,   *,   /,   %)   from   user. Using Switch case st...
Read more

sc

-
1. 3,4,5,6A represent it in array   code:-  array = [3, 4, 5, "6A"] for element in array:     print(element) 2.  show * in array   code:-   #include <stdio.h> int main() {     int array[] = { 1, 2, 3, 42};     printf("%d\n", array[0]);     printf("%d\n", array[1]);     printf("%d\n", array[2]);     printf("%c\n", array[3]);     return 0; } 3.  Calculate the no. of numerical digits in a string. code:-  s tring = "Madhav 9034, I have 34 Rubbe4." count = 0 for char in string:     if char.isdigit():         count = count + 1 print("Number of numerical digits:", count) or   def count_digits(input_string):     count = sum(1 for char in input_string if char.isdigit())     return count if __name__ == "__main__":     user_input = input("Enter a string: ")     digit_count = count_digits(user_input)   ...
Read more